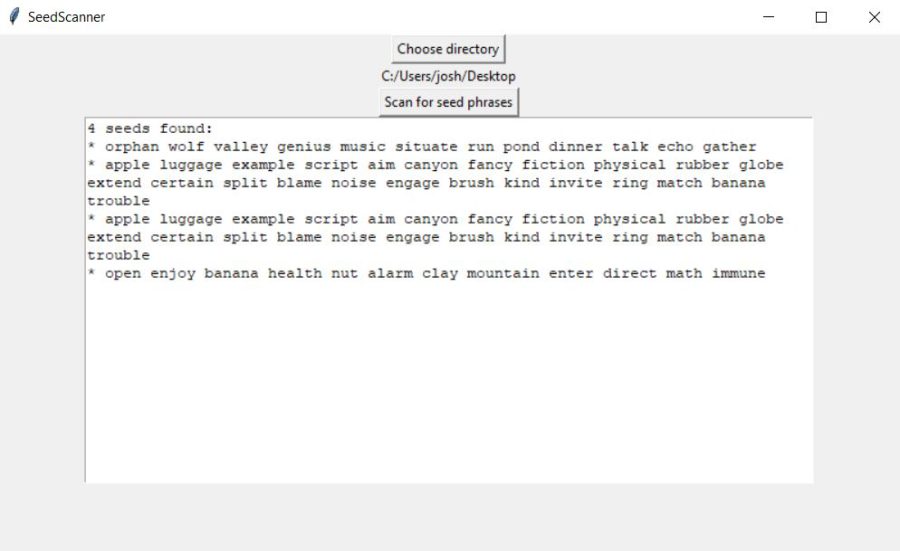
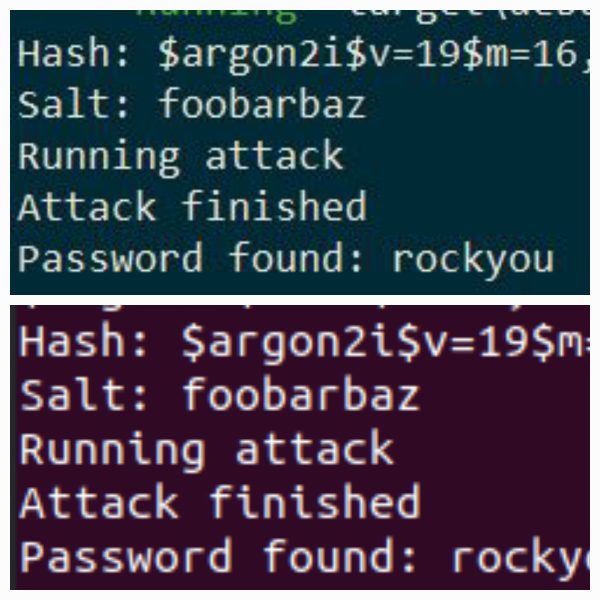
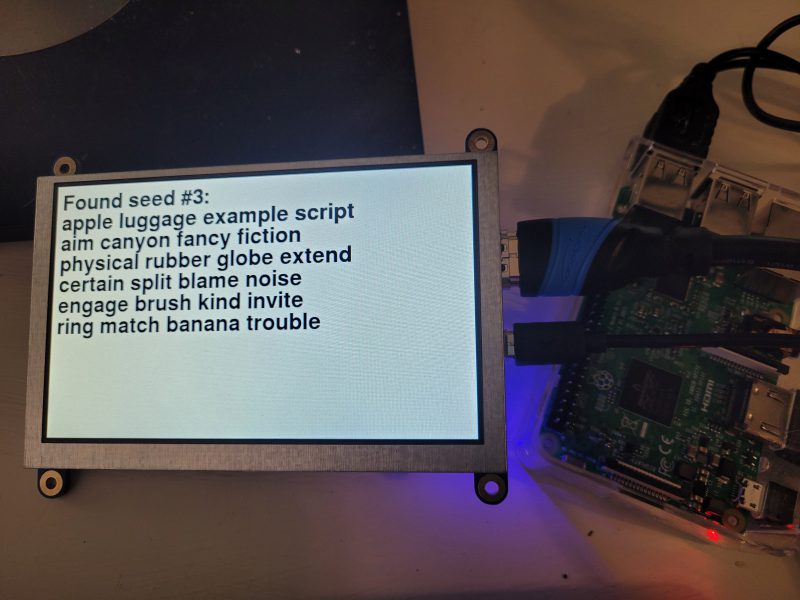
Digital Sovereignty: Protecting Your Crypto Assets Against Common Threats
EBook: https://www.amazon.com/dp/B0F3WJ6MTJ
EBook (B&N): https://www.barnesandnoble.com/w/digital-sovereignty-josh-mcintyre/1147312993?ean=2940182032216
EBook (additional retailers): https://books2read.com/digitalsovereignty
Paperback: https://www.amazon.com/dp/B0F47FMHPK
Paperback (B&N): https://www.barnesandnoble.com/w/digital-sovereignty-josh-mcintyre/1147312993
Direct USD or Crypto (EBook & Paperback): https://chaintuts.store
Open Source Repo (Individual Chapters): https://github.com/chaintuts/crypto-book
Code
All of my code can be viewed on my Github: https://github.com/chaintuts
Many code projects with different technologies, covering everything from cryptocurrencies to cybersecurity to hobby interests and more!
This code: see repositories for detailed licenses. All projects use the BSD 2-clause License.Sharing and reuse (with attribution) is highly encouraged!
Videos
All videos are available under the CC-BY 4.0 license.Sharing and reuse (with attribution) is highly encouraged!
chaintuts Tech Education
My chaintuts Youtube channel link
Josh’s Active Adventures
My Josh’s Active Adventures channel link
Photos
All of my photos can be viewed on my Flickr page: https://flickr.com/joshmcintyre
All photos are available under the CC-BY 4.0 license.Sharing and reuse (with attribution) is highly encouraged!